慣性モーメント
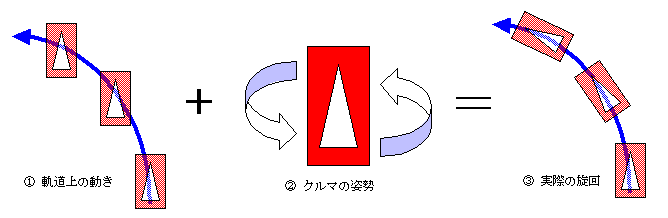
クルマの旋回を上から見ると、下図のようになる。

このとき、② クルマの姿勢 を論じる際に、クルマが回転しやすいか否かを表す物理量を慣性モーメントと
いう。(① 軌道上の動き はタイヤのグリップと遠心力が決める因子である)
回転運動は、直線運動と空間的に異なるように思えるが、力学的には全く同一の概念で取り扱うことが出来る。
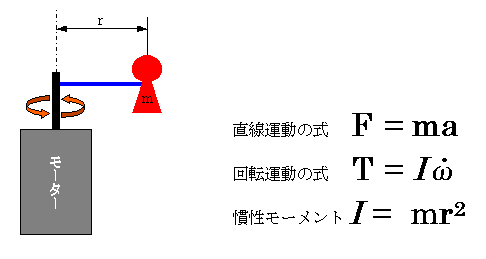
回転運動におけるトルクTは、直線運動における力Fに相当し、慣性モーメントIが、直線運動における
質量m と同じ性質を持つ。ただし慣性モーメントIには回転半径が絡んでいるため、重心mが回転中心に
近いほうが、同じ質量の物体でも慣性モーメントIは小さくなり、俊敏に回転する。
ところで、飛行機の場合は3軸それぞれの慣性モーメントについて配慮が必要となるが、クルマの場合は
基本的には水平な平面上を走るから、ヨー軸まわりの慣性モーメントのみを考慮して設計する。

このとき、ヨー軸をクルマのどの位置に立てるかが大問題となるが、これを決める因子が重心位置であり、
前後の車輪にかかる重量の比率を4:6にするように拘るのは、このためである。
高速で旋回するクルマの回転中心注)(擬似的な機械中心:上図のモーターのシャフトに相当)は、タイヤの
中心を結ぶ線の交点となる。
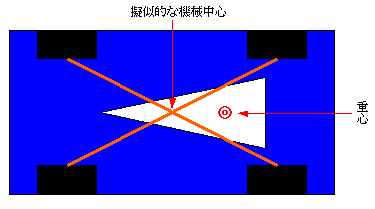
ここと重心を重ねれば、慣性モーメントは最小になるが、アクセル・ワークでクルマの姿勢を操るには、重心を
擬似的な機械中心より僅かに後寄りの設定すると、素性の良いドライブ・フィールを得る。その最適値が4:6
なのだ。 (Fulcrum 著)
--------------------------------------------------
注) 車庫入れの場合は、旋回半径が極端に小さく、慣性が問題となる速度ではないので、別な扱いをする。